Although the dire medical situation and mounting economic toll of covid-19 is of immediate and first-order importance, the virus has also prompted many to ponder their own mortality. Whether it’s doctors in emergency rooms who quickly redrafted codicils or nursing home attendants pondering their own DNR instructions, the randomness or mortality is being imprinted on our susceptible behavioral minds. Interestingly, preliminary and anecdotal evidence suggests a spike in the acquisition of life insurance policies over the last few months, perhaps as people learn to appreciate the value of this unique risk management instrument. On a historical note this is precisely what happened in the aftermath of the Spanish Flu in 1918, when the American life insurance industry began a flourishing period of remarkable growth. (See prior blog post.)
Do I need Longevity Insurance?
Unfortunately – and the launching point for this blog post is that — one of the behavioral byproducts of excess anchoring on death, is that longevity or the prospects of becoming a centenarian now appear somewhat farfetched. This is especially the case as the public continues to hear that covid-19 disproportionately impacts the elderly. One doesn’t require an MBA in marketing to know that it’s more difficult to advocate for annuities and the value of insuring (or better yet, pooling) longevity risk when the public dialogue and focus of attention is on the exact opposite: sickness and death.
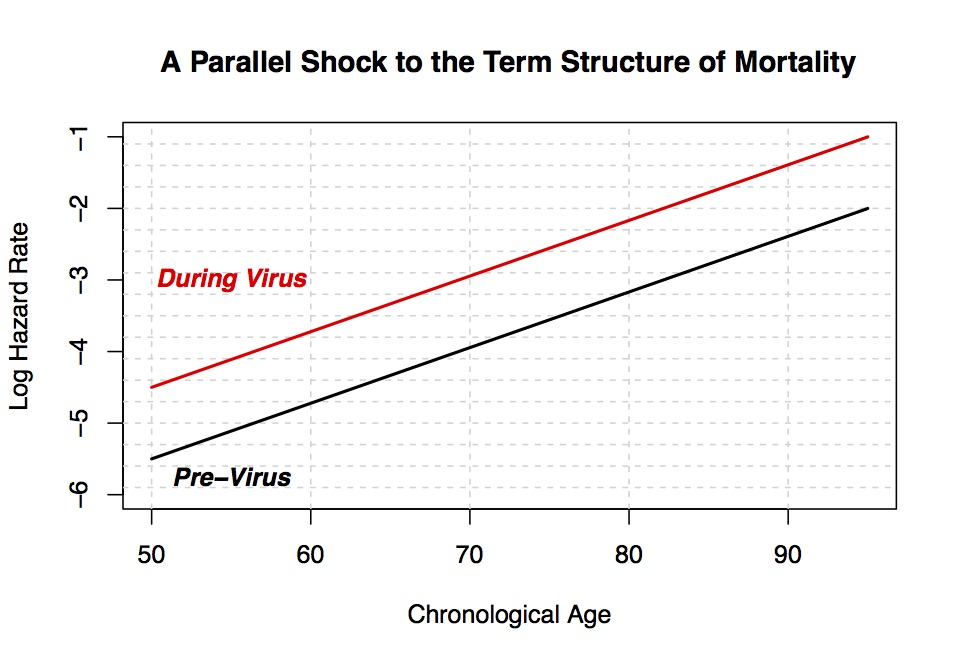
On a technical note (before I get into the more practical aspects), I should note that covid-19 appears to have increased log mortality rates in a linear manner (see above figure), which then increases mortality rates proportionally (see figure below.) I’m still working on the details and will present proper data in this upcoming seminar, but I call this a parallel shift of the term structure of mortality. For example, whereas the negligible mortality rate of a 40-year-old might have temporarily doubled from 1-in-10,000 to 1-in-5,000, the mortality rate of a 90-year-old has increased from 1-in-30 to 1-in-15. That is not insignificant. Another way to think about what covid-19 is doing, is that it increases your biological age by 8 to 10 years. See the following article for more on that concept. Think of a (chronological) 80-year-old with a mortality rate denoted by the black dot. Those are normal times. Then a horrible virus comes along and increases the mortality (curve) rate to the red dot. That point (on the y-axis) corresponds to the mortality rate of someone before the virus, who was 90-years-old chronologically. So, the 80-year-old has aged by 10 years between March and May 2020 (which, by the way, is exactly what those 3-months felt like.) What happens when the virus subsides and the red curve moves back down towards the black curve is another interesting question. Personally I think it will overshoot the black curve, but now I’m getting way too stochastic.
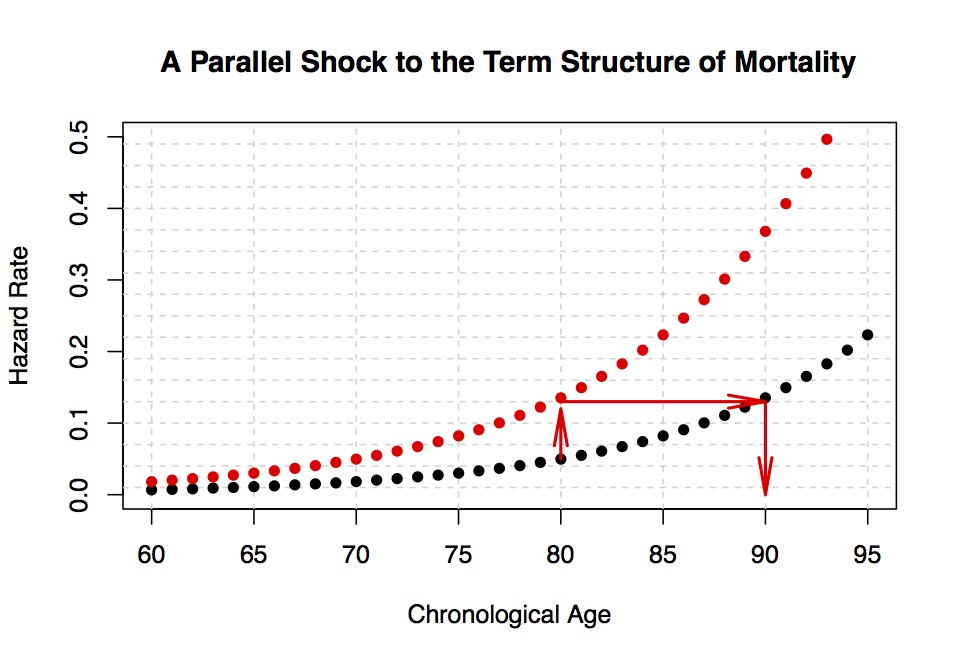
Geeky stuff aside, here is the relevant question (again.) If the public believe they aren’t living as long as before — because mortality rates have increased — how should the annuity industry continue to justify and encourage longevity insurance?
Well, here is my main idea. Counter-intuitively the magnitude of longevity risk, which technically is the coefficient of variation of your remaining life, actually increases as mortality rates spike. Moreover, if episodes of covid-19 are now part of the new non-normal then over the foreseeable future longevity risk will be higher rather than lower. Ergo, annuities will become even more important going forward. Longevity risk is not that you might live a long time (the first moment). Rather, it’s about the uncertainty around that expectation (a.k.a. second moment.)
Explaining this simple statistical idea is critical if the insurance industry hopes to convince soon-to-be retirees (and the media) to encourage protection against an event that is decades away, and less likely than before.
The following table – which will be justified in greater detail in the above noted presentation and the full length article (I promise) — illustrates this main insight using a well-established (a.k.a. Gompertzian) model of longevity. The first row represents normal times when the life expectancy of a typical (average) 65-year-old retiree is 20.11 years (living to age 85), and the standard deviation of life is 9.11 years. In the fourth column the coefficient of variation, which is the ratio of the latter to the former, is 45.3%. From a cold quantitative perspective personal (idiosyncratic) longevity risk really is just a number and for a typical 65-year-old retiree that number is 45.3%. To place that 45.3% (ok, compared to what?) in perspective, it’s actually larger than the normal volatility of the stock market VIX, or the variability of the weather on any given day in May. In fact, pension plans and insurance actuaries keep a very close eye on this number, although they compute it for pensionaries in aggregate versus individually. See reference [2] for more on that. But to be clear, this 45.3% personal longevity risk is during normal times. Now let’s examine what happens during a shock to the term structure of mortality.
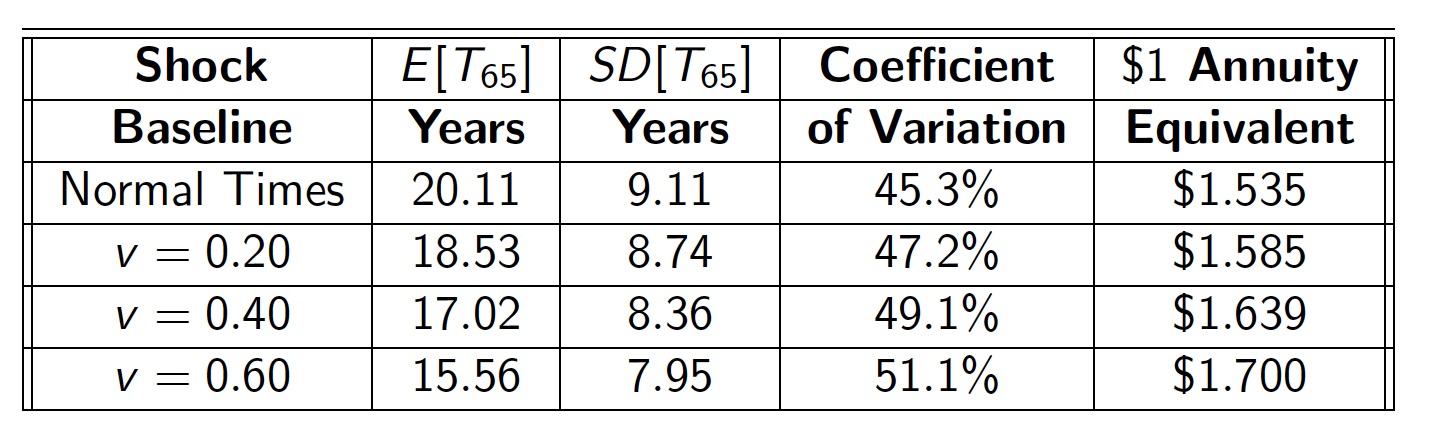
The first column of the table (starting in the second row) captures the hypothetical magnitude of the mortality shock. They represent shocks of 20%, 40% and 60% above normal mortality. The second column translates the shock units into a life expectancy (in years) for a typical 65-year-old. For example, a 20% shock to mortality rates can be viewed or interpreted as a decline of: 20.11-18.53 = 1.58 years in life expectancy. In comparison, the standard deviation of life declines by (only) a third of a year, leading to a coefficient of variation of 47.2%, which is higher than the 45.3% in normal times. Key point: The virus has increased the magnitude of longevity risk. So yes, the odds of living longer have declined somewhat due to the shock, but life is riskier – making annuities more valuable from an economic perspective. Now remember, the market price of the annuity is a completely different matter and depends on the term structure of interest rates as well as mortality. I’m talking about economic value.
How do I know that the economic value increases? Well, the fifth and final column within the table displays the so-called annuity equivalent wealth of a life annuity. This metric, which is quite popular with academic economists is explained in proper detail within the references labeled as [1], [4], [5] and [7]. But, it’s an attempt to measure how much wealth retirees would be willing to give-up for a fairly priced annuity. This isn’t a graduate course in economics, but in a nutshell the consensus is that the annuity equivalent wealth metric is the proper way of measuring the benefits of pooling longevity. And, in the table it is expressed on a value-per-dollar basis. For non-economists and non-academics, the bigger that number the more economically valuable is the annuity. That’s it.
Technical details aside (and they are important), notice how the annuity equivalent wealth increases from $1.535 to $1.585, when the longevity risk jumps from 45.3% to 47.2%. In fact, if the shock to mortality is closer to 60%, as was observed in Spain or Italy during the worst weeks of the outbreak, the coefficient of variation climbs to 51.1%, inducing the annuity equivalent wealth value of $1.7 per dollar. Both numbers move in the same direction and the practical message is the same, a sudden drop in the odds of survival increases — and certainly doesn’t reduce — the value of annuitization.
In Sum:
As noted above, this brief blog post is part of a longer article and presentation which attempts to explain (and justify) the rather subtle insight that covid-19 increases the economic benefits of annuitization, both in terms of conventional longevity risk management as well as protection against volatile markets. Of course, this also raises the question of whether you actually need more longevity insurance to begin with, which obviously depends on pre-existing annuity income vis a vis mortality heterogeneity. See reference [3] as well as [5] for more on that, since this isn’t the place to debate who doesn’t need more annuity income. In sum, don’t let a virus scare you away from thinking about longevity — as well as insurance.
References
[1] Brown, J. R. (2001). Private pensions, mortality risk, and the decision to annuitize. Journal of Public Economics, 82(1), 29-62.
[2] Dushi, I., Friedberg, L. & Webb, T. (2010). The impact of aggregate mortality risk on defined benefit pension plans, Journal of Pension Economics and Finance, Cambridge University Press, vol. 9(4), pages 481-503, October.
[3] Gong, G., & Webb, A. (2008). Mortality heterogeneity and the distributional consequences of mandatory annuitization. Journal of Risk and Insurance, 75(4), 1055-1079.
[4] Kotlikoff, L. J., & Spivak, A. (1981). The family as an incomplete annuities market. Journal of political economy, 89(2), 372-391.
[5] Milevsky, M. A. (2020). Swimming with wealthy sharks: longevity, volatility and the value of risk pooling. Journal of Pension Economics & Finance, 19(2), 217-246.
[6] Milevsky, M.A. (2019), Longevity Insurance for a Biological Age: Why Your Retirement Plan Shouldn’t Be Based on the Number of Times You Have Circled the Sun, ISBN: 9781-7906-58268.
[7] Yaari, M. E. (1965). Uncertain lifetime, life insurance, and the theory of the consumer. The Review of Economic Studies, 32(2), 137-150.
